
Characterization of highly divergent optics (DOC)
Project focus
- Wavefront Measurement Device for Highly Divergent Optics
- Wavefront Stitching and Reconstruction from Segmented Measurements
- Automatic Characterization of an Optical Device
Description
Opto-mechatronic devices such as triangulation sensors or confocal chromatic sensors project focused light beams onto the surface of the measuring object. Assessing the properties of the focused beam is essential as they are directly related to the achievable measurement resolution and precision of the opto-mechatronic device. Such properties can be evaluated by measuring the optical aberrations of the focused beam, since they directly deliver information about the defects in the optical system. To characterize or to improve the optical system, an exact knowledge of the involved optical aberrations is therefore crucial.
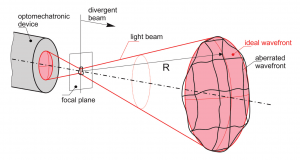
The focused spot produced by the mechatronic device can be examined by analyzing the resulting spherical wavefront.
One approach to derive the optical aberrations of an optical system is to measure the surface geometry of single components by surface profilers such as deflectometers, interferometers and tactile or non-tactile measuring machines, determining their relative alignment within the optical path and make use of simulation tools to obtain the aberrations of the entire optical system. With an increasing number of involved optical components, this approach becomes complex, time-consuming and does not allow a direct characterization of the optical quality after assembling the entire optical system.
Instead, measuring the wavefront of the focused beam emitted by the optical system allows to directly characterize the optical aberrations of the entire system, as depicted in Figure 1. A wavefront describes a surface composed of points of equal phase of the optical field within an optical wave. Each component inside the optical path contributes to the shape of the wavefront that can be measured by wavefront sensing devices. To determine the optical aberrations of the system, the measured wavefront is then compared to an ideal, aberration-free wavefront. Wavefront sensing is currently used in a whole variety of applications such as:
- optical shop testing to determine the quality of lenses,
- measuring the dynamic deformation of surfaces such as scanning mirrors,
- in production lines to characterize the surface topology of wafers, flat panels and glass sheets,
- in astronomy as part of a closed loop system to improve image quality, and
- in medical imaging for determining eye aberrations.
Scanning wavefront sensor
The research in this area also deals with a fundamental aspect of optics: The problem of directly assessing the shape of a light wave. The available tools – optical devices themselves – are not yet fit to deal with curved wavefronts. To overcome the limitations of the available sensor types they are integrated with high-precision positioning systems. By merging the wavefront data with the corresponding positioning and alignment data, a representation of the global wavefront can be achieved. The development of suitable reconstruction and stitching methods forms another central challenge of this research project.
Figure 2 depicts an experimental setup to investigate the properties of a scanning wavefront sensor. By repositioning and reorienting the sensor, its limitations concerning the opening angle of the wavefront under test can be circumvented.
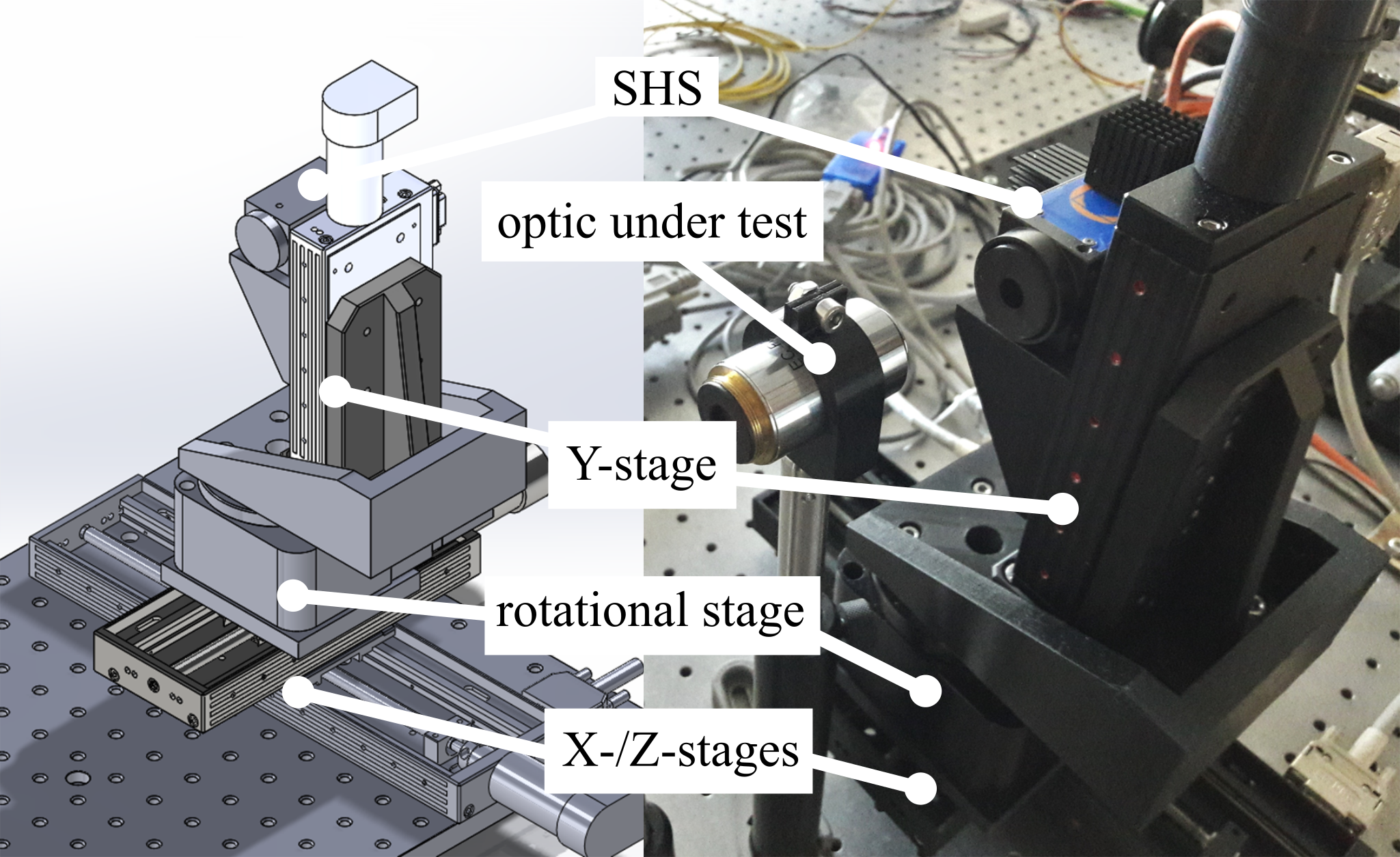
Shack-Hartmann sensor on a scanning setup.
Wavefront Reconstruction
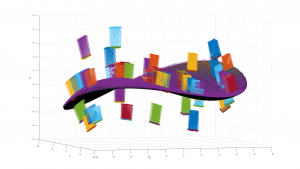
With such a setup, a more or less arbitrary wavefront can be recorded by taking multiple, partially overlapping measurements. These measurements then have to be combined with the position data to form a representation of the global wavefront. Figure 3 shows a representation of such a curved wavefront which could not be acquired directly with a single, static sensor.

3D representation of a highly-divergent wavefront, reconstructed from 15 individual, partially overlapping measurements.
However, due to several positioning errors the sensor positions might be faulty which leads to a challenge of reconstructing the entire wavefront. Hence, sophisticated wavefront reconstruction algorithms have to be developed in order to get a well reconstructed wavefront despite these errors. Such algorithms mainly utilize estimation methods and digital image processing techniques like stitching, feature detection etc.
To facilitate the development of such algorithms a software that simulates the wavefront measurement with a Shack-Hartmann sensor is developed too (Figure 4).
Simulation of measurement of a wavefront with a scanning Shack-Hartmann sensor.
Applications
- Characterization of freeform optical parts (e.g. modern smartphone lenses)
- Automatic characterization of optical components or assemblies
- In-line quality assurance
Related publications
- N. Berlakovich, M. Fuerst, E. Csencsics, and G. Schitter, Robust wavefront segment registration based on a parallel approach, Applied Optics, vol. 60, iss. 6, p. 1578–1586, 2021.
[BibTex] [Download]@article{TUW-295213, author = {Berlakovich, Nikolaus and Fuerst, Martin and Csencsics, Ernst and Schitter, Georg}, title = {Robust wavefront segment registration based on a parallel approach}, journal = {Applied Optics}, year = {2021}, volume = {60}, number = {6}, pages = {1578--1586}, doi = {10.1364/AO.413207} }
- M. Fuerst, E. Csencsics, N. Berlakovich, and G. Schitter, Automated Measurement of Highly Divergent Optical Wavefronts with a Scanning Shack-Hartmann Sensor, IEEE Transactions on Instrumentation and Measurement, vol. 70, 2021.
[BibTex] [Download]@article{TUW-291040, author = {Fuerst, Martin and Csencsics, Ernst and Berlakovich, Nikolaus and Schitter, Georg}, title = {Automated Measurement of Highly Divergent Optical Wavefronts with a Scanning Shack-Hartmann Sensor}, journal = {IEEE Transactions on Instrumentation and Measurement}, year = {2021}, volume = {70}, numpages = {9}, doi = {10.1109/TIM.2020.3038002}, keywords = {Shack-Hartmann wavefront sensor, Dynamic range extension, Optical metrology, Automatic optical inspection, Quality management, Error Budgeting} }
- M. Fuerst, N. Berlakovich, E. Csencsics, and G. Schitter, Self-Aligning Scanning Shack-Hartmann Sensor for Automatic Wavefront Measurements of High-NA Optics, in Proceedings of the IEEE International Instrumentation and Measurement Technology Conference (I2MTC 2020), 2020.
[BibTex] [Download]@inproceedings{TUW-289906, author = {Fuerst, Martin and Berlakovich, Nikolaus and Csencsics, Ernst and Schitter, Georg}, title = {Self-Aligning Scanning Shack-Hartmann Sensor for Automatic Wavefront Measurements of High-NA Optics}, booktitle = {Proceedings of the IEEE International Instrumentation and Measurement Technology Conference (I2MTC 2020)}, year = {2020}, numpages = {6}, doi = {10.1109/I2MTC43012.2020.9128499}, keywords = {Shack-Hartmann wavefront sensor, Dynamic range extension, Optical metrology, Automatic optical inspection, Quality management}, note = {Vortrag: IEEE International Instrumentation and Measurement Technology Conference Proceedings I2MTC (2020), Dubrovnik, Kroatien; 2020-05-25 -- 2020-05-28} }
- M. Fuerst and G. Schitter, Scanning Wavefront Sensor for Measurement of Highly Divergent Wavefronts, in Proceedings of the Joint Conference 8th IFAC Symposium on Mechatronic Systems (MECHATRONICS 2019), and 11th IFAC Symposium on Nonlinear Control Systems (NOLCOS 2019), 2019.
[BibTex] [Download]@inproceedings{TUW-281663, author = {Fuerst, Martin and Schitter, Georg}, title = {Scanning Wavefront Sensor for Measurement of Highly Divergent Wavefronts}, booktitle = {Proceedings of the Joint Conference 8th IFAC Symposium on Mechatronic Systems (MECHATRONICS 2019), and 11th IFAC Symposium on Nonlinear Control Systems (NOLCOS 2019)}, year = {2019}, journal = {IFAC-PapersOnLine/Elsevier}, volume = {52/15}, numpages = {6}, doi = {10.1016/j.ifacol.2019.11.644}, keywords = {Freeform optics, optical metrology, wavefront measurement, scanning system, Shack-Hartmann sensor, surface metrology}, note = {Vortrag: Joint Conference 8th IFAC Symposium on Mechatronic Systems (MECHATRONICS 2019), and 11th IFAC Symposium on Nonlinear Control Systems (NOLCOS 2019), Wien; 2019-09-04 -- 2019-09-06} }
- M. Fuerst, S. Unger, S. Ito, and G. Schitter, Wavefront measurement based feedback control for automatic alignment of a high-NA optical system, Journal of Physics: Conference Series, vol. 1065, 2018.
[BibTex] [Download]@article{TUW-273524, author = {Fuerst, Martin and Unger, Severin and Ito, Shingo and Schitter, Georg}, title = {Wavefront measurement based feedback control for automatic alignment of a high-NA optical system}, journal = {Journal of Physics: Conference Series}, year = {2018}, volume = {1065}, numpages = {4}, doi = {10.1088/1742-6596/1065/3/032001} }
- M. Fuerst, S. Unger, S. Ito, and G. Schitter, Wavefront measurement based feedback control for automatic alignment of a high-NA optical system, in XXII World Congress of the International Measurement Confederation (IMEKO), 2018.
[BibTex] [Download]@inproceedings{TUW-271223, author = {Fuerst, Martin and Unger, Severin and Ito, Shingo and Schitter, Georg}, title = {Wavefront measurement based feedback control for automatic alignment of a high-NA optical system}, booktitle = {XXII World Congress of the International Measurement Confederation (IMEKO)}, year = {2018}, numpages = {4}, note = {Vortrag: XXII World Congress of the International Measurement Confederation (IMEKO), Belfast (UK); 2018-09-03 -- 2018-09-06} }
- E. Csencsics, S. Ito, M. Fuerst, F. Cigarini, and G. Schitter, Christian Doppler Laboratory Precision Engineering for Automated In-line Metrology, in 1st GMAR workshop, 2017.
[BibTex]@Conference{TUW-0612172, author = {Csencsics, E. and Ito, S. and Fuerst, M. and Cigarini, F. and Schitter, G.}, title = {Christian Doppler Laboratory Precision Engineering for Automated In-line Metrology}, booktitle = {1st GMAR workshop}, year = {2017} }
Project Partners
Funding
Contact
Univ.-Prof. Dipl.-Ing. Dr.sc.techn. Georg SchitterDDipl.-Ing. Martin Fuerst
Dipl.-Ing. BSc Nikolaus Berlakovich
Project Staff
DDipl.-Ing. Martin FuerstDipl.-Ing. BSc Nikolaus Berlakovich