
Modeling and control of a four-high heavy plate rolling mill
Project focus
- Modeling, identification, and analysis of mechanical and hydraulic components of a finishing mill
- Control of heavy plate mills (feedforward thickness control)
- Online-Adaptation of model parameters for model based control
Description
In heavy plate rolling, the heated plates are plastically deformed by rolling mills. For this task, reversing four-high mill stands consisting of two work-rolls and two backup-rolls are often used. The plate is deformed between the two work-rolls in several rolling passes. The high rolling forces during the deformation cause the work-rolls to bend which in turn yields a nonuniform thickness profile of the plate. The two backup-rolls reduce the bending deflection of the work-rolls. Additionally, the mills are equipped with devices for bending compensation like hydraulic bending systems and/or specifically shaped rolls (CVC-rolls). These measures shall ensure a plain roll gap and thus a uniform lateral thickness profile of the final product.

Four-high rolling mill, © Dillinger Hüttenwerke AG.
During the rolling process, the mill is loaded with forces up to 90 MN, which cause elastic deformations of the mill up to 13 mm. The total deflection consists of the elastic deformation of the mill, the bending deflection of the rolls, and the compression of the rolls. As thickness tolerances of 0.1 mm have to be met, it is necessary to compensate the deflection. Furthermore, the mill has to be set up in such a way that the roll gap between the two work-rolls is as flat as possible to ensure a uniform exit thickness of the plate in lateral direction. However, the exit thickness of the plate cannot be reliably measured close to the roll gap due to the hostile environment (heat, steam). The thickness measurement, which is located some meters away from the mill stand, is not useful for real-time thickness control due to the time lag. Thus, the exit thickness has to be calculated with a mathematical model. The model has to include the compliance of the hydraulic and the mechanical components of the mill stand and – especially for the calculation of the thickness profile in lateral direction – the bending and the compression of the rolls. The model results may then be used for real-time control.
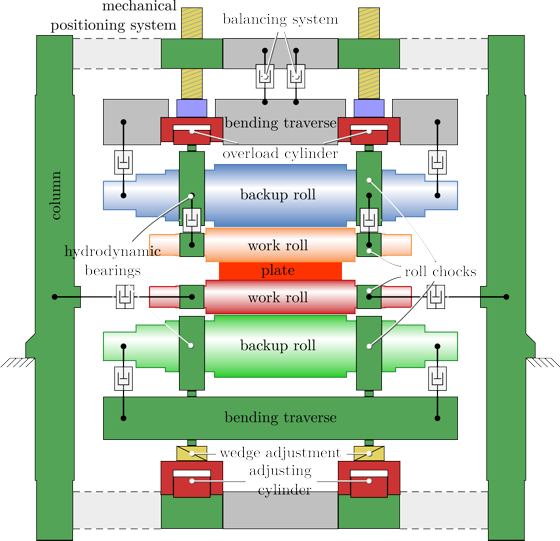
Setup of a four-high finishing mill – front view.
Due to the dimensions of the rolls, a deflection model based on the Timoshenko beam theory is used. To fully describe the problem, the loads of the rolls and the boundary conditions have to be determined.
The rolling force is the force between the two work-rolls required for the plastic deformation of the plate. This force depends on the material of the plate, the rolling velocity, the temperature distribution as well as the entry and exit thickness profile of the plate. As the exit thickness depends on the bending of the two work-rolls, a nonlinear coupling of the differential equations of the work-rolls is obtained.
Similar considerations may be made about the contact of the work- and backup-rolls. Generally, there is a nonlinear relation between the contact force and the bending of the work- and backup-rolls.
To determine the boundary conditions, the distance between the backup-roll journals has to be identified. Apart from a calibration of the model, this requires the calculation of the deflection of the mill stand which depends on the rolling force. Moreover, friction forces between the roll chocks and the columns have to be taken into account. Furthermore, the position of the backup-roll journals in the hydrodynamic bearings, which depends nonlinearly on the rolling force and the rolling velocity, has to be determined.
A 2-point boundary value problem consisting of 16 coupled nonlinear differential equations has to be solved. As the model is to be used for real-time control, its calculation time must not exceed the sampling period of the system.
The developed solution has been successfully verified with measurement data from an industrial finishing mill.
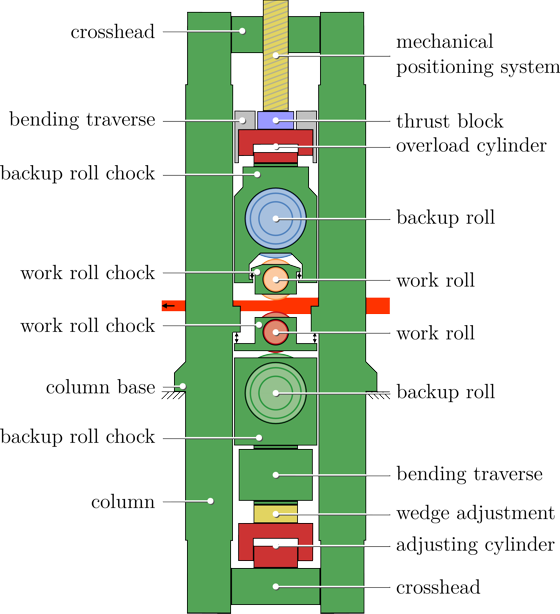
Setup of a four-high finishing mill – side view.
If such a model is used in a conventional feedback controller, it is difficult to compensate for fast variations of the entry thickness and the yield strength of the plate due to the limited response characteristic of the positioning system and the closed-loop control. Thus, strategies to estimate the entry thickness and yield strength profile during a pass here developed. By applying these profiles in the sense of a feedforward control to the next pass, it is possible to partially compensate the thickness deviations in the entry profiles.
The developed solutions were tested in computer simulations before they were applied to an industrial finishing mill stand where they are further developed successfully.
Selected publications
- T. König, Entwicklung, Parametrierung und Online-Adaption eines mathematischen Modells eines Walzgerüstes beim Warmwalzen, A. Kugi and K. Schlacher, Eds., Aachen: Shaker Verlag, 2014, vol. 22.
[BibTex]@Book{Koenig14, Title = {Entwicklung, {P}arametrierung und {O}nline-{A}daption eines mathematischen {M}odells eines {W}alzger{\"u}stes beim {W}armwalzen}, Author = {K{\"o}nig, T.}, Editor = {A. Kugi and K. Schlacher}, Publisher = {Shaker Verlag}, Year = {2014}, Address = {Aachen}, Series = {Modellierung und Regelung komplexer dynamischer Systeme}, Volume = {22}, ISBN = {978-3-8440-3224-6}, Organization = {Institute f{\"u}r Automatisierungs- und Regelungstechnik (TU Wien) und Regelungstechnik und Prozessautomatisierung (JKU Linz)}, } - T. König, A. Steinboeck, and A. Kugi, Online Calibration of a Mathematical Model for the Deflection of a Rolling Mill, in Proceedings of Rolling 2013, Venezia, Italy, 2013, p. 1–12.
[BibTex]@InProceedings{Konig13, author = {T. K{\"o}nig and A. Steinboeck and A. Kugi}, title = {{{O}nline {C}alibration of a {M}athematical {M}odel for the {D}eflection of a {R}olling {M}ill}}, booktitle = {Proceedings of Rolling 2013}, year = {2013}, month = {6}, pages = {1--12}, address = {Venezia, Italy}, } - T. König, A. Steinboeck, A. Kugi, R. Heeg, and T. Kiefer, Deflection and bending model of a four-high mill stand for heavy plate rolling, in Proceedings of the 4th International Conference on Modelling and Simulation of Metallurgical Processes in Steelmaking, STEELSIM, METEC InSteelCon 2011, Düsseldorf, Germany, 2011.
[BibTex]@InProceedings{Koenig11, author = {T. K\"onig and A. Steinboeck and A. Kugi and R. Heeg and T. Kiefer}, title = {Deflection and bending model of a four-high mill stand for heavy plate rolling}, booktitle = {Proceedings of the 4th International Conference on Modelling and Simulation of Metallurgical Processes in Steelmaking, STEELSIM, METEC InSteelCon 2011}, year = {2011}, month = {6}, address = {D\"usseldorf, Germany}, } - R. Heeg, Modellierung und Dickenregelung beim Warmwalzen, A. Kugi and K. Schlacher, Eds., Aachen: Shaker Verlag, 2009, vol. 5.
[BibTex]@Book{Heeg09, Title = {Modellierung und Dickenregelung beim Warmwalzen}, Author = {R. Heeg}, Editor = {A. Kugi and K. Schlacher}, Publisher = {Shaker Verlag}, Year = {2009}, Address = {Aachen}, Series = {Modellierung und Regelung komplexer dynamischer Systeme}, Volume = {5}, ISBN = {978-3-8322-7871-7}, } - T. König, Mathematische Modelle zur Berechnung der Auffederung eines Fertiggerüstes, 2008.
[BibTex]@Mastersthesis{koenig08, Title = {Mathematische Modelle zur Berechnung der Auffederung eines Fertigger{\"u}stes}, Author = {K{\"o}nig, T.}, School = {Vienna University of Technology}, Year = {2008}, } - R. Heeg, T. Kiefer, and A. Kugi, Control of Plate Thickness in Heavy Plate Mills: A New Perspective, in Proceedings of the 12th IFAC Symposium on Automation in Mining, Mineral and Metal Processing, Quebec City, Canada, 2007, p. 107–112.
[BibTex]@InProceedings{Heeg07, author = {R. Heeg and T. Kiefer and A. Kugi}, title = {Control of Plate Thickness in Heavy Plate Mills: A New Perspective}, booktitle = {Proceedings of the 12th IFAC Symposium on Automation in Mining, Mineral and Metal Processing}, year = {2007}, month = {8}, pages = {107--112}, doi = {10.3182/20070821-3-CA-2919.00016}, address = {Quebec City, Canada}, }
Applications
- Rolling mill automation
- Plastic deformation process
- Hot plate rolling
Related Projects
- Lateral guiding and shape control in heavy plate rolling
- Modeling and control of a four-high heavy plate rolling mill
- Modeling and control of hot levelers
- Thermal model and optimal time scheduling of hot rolling
- Optimization of process times and product sequences in a hot-rolling mill with batch-type reheating furnaces